How to make the best decision in uncertain situations

Red and Green Guide:

Mastering risk is the most solid confidence when facing uncertain events. As Warren Buffett insightfully observed: "Risk comes from not knowing what you're doing." Therefore, when confronting risk, Buffett chooses to "multiply the probability of profit by the potential profit amount, subtract the probability of loss multiplied by the potential loss amount," making the "unknown" calculable and optimizable before making decisions.

Excerpted from "Bayes' Theorem"

Source: Geshang Private Equity Circle

First, let's get to know the famous Bayes' Theorem:

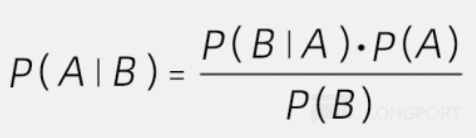
Prior Probability P(A): The initial probability of event A before observing new evidence B.

Likelihood P(B∣A): The probability of observing evidence B given that event A has occurred.

Marginal Probability P(B): The total probability of evidence B under all possible circumstances (usually calculated via the law of total probability).

Posterior Probability P(A∣B): The updated probability of event A after observing B.

In plain language, the four parts of the formula can be explained as:

(The probability of event A occurring given that event B has occurred) = (The probability of event B occurring given that event A has occurred) × (The probability of event A occurring alone) ÷ (The probability of event B occurring alone).

Bayes' Theorem is a very peculiar theorem. Its expression is extremely concise, involving only multiplication and division. Its proposer was merely an ordinary wealthy gentleman from the 18th century who studied mathematics as a hobby. Despite this, Bayes' Theorem has had an extraordinarily profound impact—it can explain why even if 99% of people who test positive for cancer don't have it, the test's accuracy can still be as high as 99%; why DNA matching has only a one in twenty million chance of being wrong, yet it can still lead to wrongful convictions with high probability; why a scientific conclusion may have "statistical significance" but still has a high probability of being wrong.

AI is essentially a specific application of Bayes' Theorem. At its most fundamental level, what AI does is "predict." An AI application that can distinguish between images of cats and dogs is essentially "predicting" human judgments based on past training data and current image information. Those AIs that chat with you and generate high-quality images are also making predictions at their core—they're predicting how human writers or artists would respond to those prompts. The foundation of these predictive behaviors is Bayes' Theorem.

Therefore, every time we make decisions in the face of uncertainty, we can use Bayes' Theorem to assess to what extent the decision is a good one. It describes how to update beliefs using new evidence given known prior probabilities. And Bayesian decision-making thinking stems from this core idea. It is a decision-making method based on probabilistic reasoning, the essence of which is using Bayes' Theorem to update probability distributions to make optimal decisions.

In the decision-making process, Bayesian decision theory combines this probability updating process with decision rules to minimize expected loss or maximize expected utility.

So, how can Bayes' Theorem be truly applied in decision-making?

If we don't view Bayes' Theorem as a rigid, dogmatic mathematical tool but rather as a "probability-updating cognition" way of thinking, we can quickly grasp its essence: it doesn't pursue absolute correctness but maximizes the probability of success by continuously absorbing new information and adjusting the direction of decisions.

Next, let's look at the three realms of Bayesian thinking in broader decision-making.

1. Prior Beliefs: How to Scientify Your "Intuition"?

When making decisions, we rely not only on new information but also on prior experiential information. Generally, we call this "common sense." Every decision-maker has prior beliefs (Prior Belief), such as:

"High-end consumers value brand value more."

"During economic downturns, sales of low-priced goods will rise."

The problem with traditional decision-making is that these beliefs often become rigid dogmas, making them hard to adjust. Bayesian thinking requires quantifying prior probabilities, using data to answer "what is the historical probability of this event occurring":

"According to historical data, the probability of high-end consumers choosing brands is 70%."

"In the past three economic recessions, the probability of low-priced goods sales increasing was 80%."

This is the essence of "prior beliefs": turning vague intuition into a measurable starting point. The key point is: priors are not biases but adjustable starting points; quantify your original assumptions to avoid "I feel"-style decisions.

2. Dynamic Adjustment: How to Continuously Optimize Amid Uncertainty?

The core of Bayesian thinking is "updating old beliefs with new data." When market conditions change, decision-makers should not rigidly adhere to original strategies but calculate posterior probabilities (Posterior Probability), i.e.:

Posterior Probability ∝ Prior Probability × Weight of New Evidence

Take video recommendation algorithms as an example: platforms don't rigidly recommend "trending" content but dynamically adjust recommendations based on your viewing history (prior) and latest clicks (new data).

Another example is the new energy vehicle market: a car manufacturer initially set a "prior probability of 35% for family users in first-tier cities buying electric vehicles" based on industry reports. But when quarterly sales data showed that purchases by single white-collar workers aged 25-35 exceeded expectations by 40%, the company immediately adjusted its user profile—increasing the weight of "high-income single groups" from 15% to 30% and developing in-car smart entertainment systems accordingly.

This adjustment isn't about overturning original beliefs but fine-tuning parameters to keep the decision model aligned with market dynamics. The key point is: markets change, and so should your decision model; small-step trials + rapid iteration are more reliable than "betting on a big direction."

3. Probabilistic Thinking: Why Do Experts Never Say "Absolutely"?

Decision masters don't construct a single script but a "decision sandbox" containing multiple possibilities.

A Bayesian decision-maker wouldn't assert "this project will definitely succeed" but say: "Based on current information, the probability of success is 65%, but if competitors launch earlier, it may drop to 40%." This mindset avoids overconfidence bias (Overconfidence Bias) and prepares contingency plans before risks arise.

"Probabilistic thinking" is the ability to break down future scenarios into probability distributions. It allows decision-makers to focus on high-probability events while setting up circuit breakers for low-probability risks. The key point is: replace absolute judgments with probability ranges; decision quality depends not on outcomes but on whether the process follows Bayesian logic.

In Fact, Everyone Is a Natural Bayesian

Although in some carefully designed scenarios, people easily exhibit behavioral biases, and although most people aren't adept at complex Bayesian calculations, in most everyday situations, our decisions align remarkably well with Bayes' Theorem.

Because the brain's job is to analyze this information and infer its causes. When prediction errors occur, the brain continuously updates predictions based on new signals, striving to reduce errors and align the predictive model with reality—this remains a Bayesian process. Predictions are prior probabilities, sensory data are likelihood functions, and updated predictions are posterior probabilities.

And crucially, although your predictions constantly update based on sensory information, you essentially live in your predictions, not the data—what you experience isn't sensory data but internal predictions.

Fundamentally, our "experience" is a Bayesian model built on sensory data. Thus, consciousness itself is a Bayesian analytical model.

Everything related to decision-making involves Bayesian models because they optimally integrate new information with prior judgments. Viewing the world through Bayesian thinking, you'll find many phenomena become easier to explain.

Of course, Bayes' Theorem is hard to apply perfectly in the real world. The prior probabilities we rely on for decisions are only approximations. The decisions you (or others, institutions, decision models) make are, in reality, approximations.

But, Bayes' Theorem is the theoretical foundation for making optimal decisions under uncertainty. The more a decision aligns with the Bayesian model, the better it performs, and vice versa.

More accurately, Bayes' Theorem represents ideal decision-making; the extent to which a decision-maker follows it determines how correct the decision is.

In fact, no matter the decision process, no matter how much influence you exert on the world to achieve a goal, no matter how limited your information, whether you're a bacterium seeking high-glucose environments, a gene propagating genetic information through replication, or a government striving for economic growth—if you want to do things well, you can't escape Bayes' Theorem.

In short, in the VUCA era, Bayesian thinking provides an "evolving" decision-making framework:

Start with priors (quantify your initial judgments)

Dynamically adjust (continuously update beliefs with new data)

Make probabilistic decisions (manage uncertainty, don't eliminate it)

The future belongs to probabilistic thinkers—they never say "absolutely correct" but get closer to the truth than their opponents. In an uncertain world, the greatest certainty is mastering the wisdom of "coexisting with uncertainty."